Modelos numéricos – Fundamentos (1 de 6)

A modelagem numérica de ambientes aquáticos vem cada vez mais sendo empregada em estudos de impacto ambiental e em projetos de engenharia, como: construção e manutenção de barragens, dragagens, emissários submarinos, estudos de inundação, análises de erosão de linha de costa, projetos de engordamento de praia, estudos de autodepuração do corpo hídrico, entre muitos outros.

Muito se mostra dos resultados alcançados, mas pouco se fala dos seus fundamentos e do processo completo de implementação de um modelo numérico.

E é isso que vou começar a fazer por aqui nessa seção do blog chamada “Por dentro do modelo”.

Vai ser uma série de 7 posts (por enquanto) que vai trazer informações sobre os conceitos básicos de um modelo numérico, estrutura de implementação, principais bases de dados utilizadas para forçamento, processo de calibração, modelos mais utilizados no mundo e por aí vai.

A ideia é começar do básico, dos fundamentos, e aos poucos ir aprofundando. Primeiro porque é o caminho mais lógico. E segundo porque acredito que facilitará o processo de compreensão dos assuntos mais complexos que virão lá na frente.

Primeiro, o que é um modelo?

“Entende-se por modelo a reprodução abstrata, conceitual, gráfica ou visual de algumas
ou todas as características físicas de um comportamento natural em escala adequada (Wendland & Rüber, 1998). “

Ou seja, um modelo busca reproduzir, em escala reduzida, o ambiente ou processo que deseja ser estudado. Basicamente uma maquete realista do ambiente. O modelo pode ser:

• Físico: representa o sistema por meio de um protótipo em escala menor
• Matemático: representa a natureza via equações matemáticas

Modelos físicos

Modelos físicos referem-se ao uso de modelos de laboratório construídos em uma escala apropriada para investigar o processo de interesse. O tamanho da instalação (que pode variar de micro a grande escala) depende da escala e do fenômeno a ser modelado. A seleção da escala deve garantir que as forças dominantes estejam bem representadas.

Há quem diga que o primeiro modelo físico hidrodinâmico da história foi feito por Arquimedes (287-212 a.c), naquela clássica história que depois de sentir seu corpo flutuar na banheira saiu nu gritando Eureka! Eureka! pelas ruas de Sicília. Os fatos verdadeiros desta história são contados nesse TED de 4 minutos que vale super a pena ser visto. A partir de um desafio imposto pelo rei de construir um navio imenso, Arquimedes esboçou a lei da flutuabilidade, que ficou conhecida depois como “Princípio de Arquimedes”.

Mas voltemos ao mundo atual.

Hoje, os modelos físicos são amplamente utilizados na engenharia mecânica, civil e naval, para projetar por exemplo: navio, plataforma de petróleo, usinas hidrelétricas, barragens, bombas e eclusas. E também, em menor escala, para estudar processos hidráulicos específicos, como quebra da onda, velocidade de sedimentação, turbulência, entre outros.

E muitos destes estudos feitos em modelos físicos são essenciais para a criação e calibração dos nossos queridos modelos numéricos. Não coincidentemente, dois importantes laboratórios que possuem tanques para criar e estudar modelos físicos continuamente são também os detentores de modelos numéricos robustos amplamente utilizados pela comunidade científica e empresas (falaremos em outro post destes modelos).

A Deltares, sediada na Holanda, possui o Delta Flume. Tanque com 290 metros de comprimento, 5 de largura e 9,5 de profundidade, utilizado especialmente em projetos de engenharia de combate à inundações. A COPPE/UFRJ, no Rio de Janeiro, possui o LabOceano. O tanque mais profundo do mundo com 15 metros de profundidade no seu poço central. Capacidade que o permite simular processos de ambiente oceânico profundo sendo muito procurado pela indústria offshore.

As principais vantagens dos modelos físicos são:

• Mensurabilidade e observação: experimentos para observar e isolar fenômenos difíceis de medir na natureza,
• Repetibilidade: experimentos repetidos, para investigar a faixa de incerteza inerente aos fenômenos;
• Controle de entrada: experimentos com várias séries temporais de entrada realistas, para, por exemplo, avaliar a capacidade preditiva de modelos numéricos;
• Controle de processo: experimentos para situações simples, a fim de validar os resultados das análises teóricas de comportamento.

Modelos numéricos

Os modelos numéricos funcionam tanto como uma alternativa quanto um complemento aos modelos físicos. Apresentam grandes vantagens em relação a custos e tempo de resposta quando comparados aos modelos físicos. Porém, assim como nos modelos físicos, também possuem limitações relacionadas com as hipóteses que estão na base da teoria matemática e na reprodutibilidade de alguns fenômenos físicos envolvidos nos processos a serem simulados.

O modelo numérico quando aplicado para um problema real deve traduzir e representar o fenômeno que está ocorrendo no mundo físico. Entretanto, nem sempre isso é fácil. Ao se tentar representar um fenômeno do mundo físico por meio de equações matemáticas, raramente se tem uma descrição correta deste fenômeno. Normalmente, são necessárias várias simplificações do mundo físico para que se tenham formulações com as quais se possa trabalhar.

O emprego dos modelos numéricos está concentrado nas áreas de engenharia e ciências da terra e do mar. Como exemplo de aplicação, temos: estudos de combustão, aerodinâmica, previsão climática, poluição ambiental, propagação de ondas marinhas, entre outros.  

Hoje, um modelo numérico é baseado numa tríade composta por (Do Carmo, 2004):

• Formulação matemática (ou modelo matemático, são as equações que representam os princípios físicos do processo);
• Implementação de técnicas numéricas que permitem resolver as equações matemáticas;
• Elaboração de uma estrutura computacional (software) que permite resolver de forma ágil as equações já discretizadas numericamente.

1. Formulações matemáticas

O conjunto de equações matemáticas que está inserido no modelo numérico irá depender de quais processos físicos aquele modelo resolve. Podendo incluir qualquer processo das grandes áreas da física clássica como cinemática (movimento), dinâmica, mecânica, estática, termodinâmica e ondulatória.

E sobre este conjunto de equações, que resolvem a questão física do meio, ainda podem serem aplicadas formulações que resolvem processos químicos, biológicos, ecológicos, entre outros. Expandindo ainda mais as possibilidades de aplicação de modelos numéricos.

Geralmente, quando um modelo resolve mais de um processo, o modelo é divido em módulos (um para cada conjunto de equações) que se comunicam. Mas a base, a parte física do meio, sempre será a primeira a ser resolvida.

2. Técnicas de cálculo numérico

A análise numérica é o estudo de algorítimo de aproximação para a solução de problemas matemáticos. A solução numérica de um problema segue a seguinte estrutura (Franco, 2011):

• Modelo matemático: construído a partir da observação do fenômeno, usando leis da física e da matemática. Julga-se que esse modelo represente muito apropriadamente o comportamento real do fenômeno físico;
• Modelo numérico: obtido a partir do modelo matemático usando-se um método de aproximação para as equações diferenciais. Esse método consiste na discretização do domínio e na solução da equação em pontos específicos.

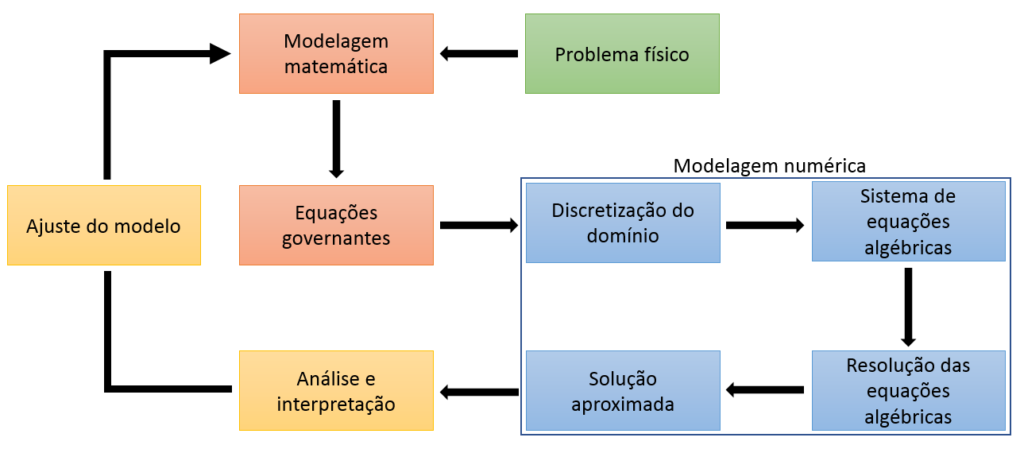
A discretização trata-se da aproximação das equações governantes do processo físico por um sistema de equações algébricas em pontos discretos no espaço (malha numérica) e no tempo.

Há diferentes métodos de discretização numérica. Os mais empregados em modelos numéricos ambientais são: Método das Diferenças Finitas (MDF), Método dos Volumes Finitos (MVF) e Método dos Elementos Finitos (MEF). 

Se quiser saber um pouco mais sobre estes métodos, este post no Blog da ESSS tem uma revisão bem didática.

3. Estrutura computacional

É válido ressaltar que os métodos numéricos e as equações de representação do processo físico já existem desde muito antes de surgirem os computadores. Inclusive, foi para facilitar a solução desses problemas matemáticos que os primeiros protótipos de computadores, as calculadoras mecânicas, foram criados. 

Mas foi a partir da disponibilidade desse processamento computacional que os modelos numéricos passaram a ser largamente utilizados, desenvolvidos e otimizados. Uma vez que cálculos maiores e mais complexos puderam ser resolvidos.

O uso do computador como ferramenta de trabalho de cálculo numérico requer o entendimento dos seus princípios de operação e de como eles interferem nos resultados obtidos. Os fatores relevantes para a escolha de um algoritmo devem envolver os aspectos de:

• Precisão desejada;
• Capacidade do método em conduzir aos resultados desejados (velocidade de convergência);
• Esforço computacional (tempo de processamento, economia de memória necessária para a resolução).

A implementação computacional consiste em, escolhida uma linguagem computacional (Fortran, Pascal, C, C++, Python, dentre outras), colocar o algoritmo elaborado em termos dessa linguagem.

Recapitulando: Um modelo numérico resolve, por meio de uma linguagem computacional e técnicas de cálculo numérico, equações (em princípio, físicas) que solucionam o processo que está sendo estudado. Para cada modelo numérico essa tríade pode ser arranjada de uma forma. Mas a estrutura será sempre a mesma. Para qualquer modelo numérico. 

Por isso é muito mais importante que se aprenda os fundamentos e não apenas a utilizar uma ferramenta (como um único software de modelo, por exemplo). Pois conhecer a estrutura e o funcionamento te possibilitará utilizar qualquer software de modelagem sem grandes dificuldades.    
 
Não se assuste caso toda essa explicação tenha ficado muito abstrata na sua cabeça. Conforme os outros posts dessa série forem sendo publicados as informações irão se encaixar e tudo ficará mais claro. 

Para ler o próximo post da série que trata da base conceitual de um modelo numérico hidrodinâmico, clique aqui. 

Fontes citadas:

ASSAD, L. P. F., et al. Noções básicas de modelagem hidrodinâmica computacional e de dispersão de poluentes. COPPE, Rio de Janeiro. 2009.

WENDLAND, E; RUBER, O. Hydrogeologic Modelle, Lehrstuhl fur Angewandte
Hydrogeologie, Ruhr, Universitat Bochum, 1998.

DO CARMO, J. S. A. Modelação em Hidráulica Fluvial e Ambiente. Imprensa da Universidade de Coimbra, Coimbra. 396 p. 2004.

FRANCO, A. T. Métodos numéricos aplicados à engenharia. Curso de Engenharia, UTFPR. Curitiba. 2011.