Calibração nada mais é do que o processo de confrontar os dados simulados com dados medidos (no caso do modelo hidrodinâmico, dados de nível e correntes) e ajustar o modelo para que este produza resultados satisfatórios.
É nessa etapa do processo de modelagem que está a “hora da verdade” para qualquer modelo. É o momento em que se pode de fato verificar e validar um dado modelo através da pergunta:
Os resultados obtidos conferem com o que se observa e se mede a respeito do fenômeno de interesse?
Para esta pergunta há duas respostas levando a duas rotas respectivamente:
- NÃO: neste caso o modelo não está validado e entra-se no processo de calibração efetivamente, com duas rotas possíveis.
- SIM: neste caso o modelo está validado e o processo de modelagem pode seguir a diante utilizando este modelo montado para as simulações desejadas.
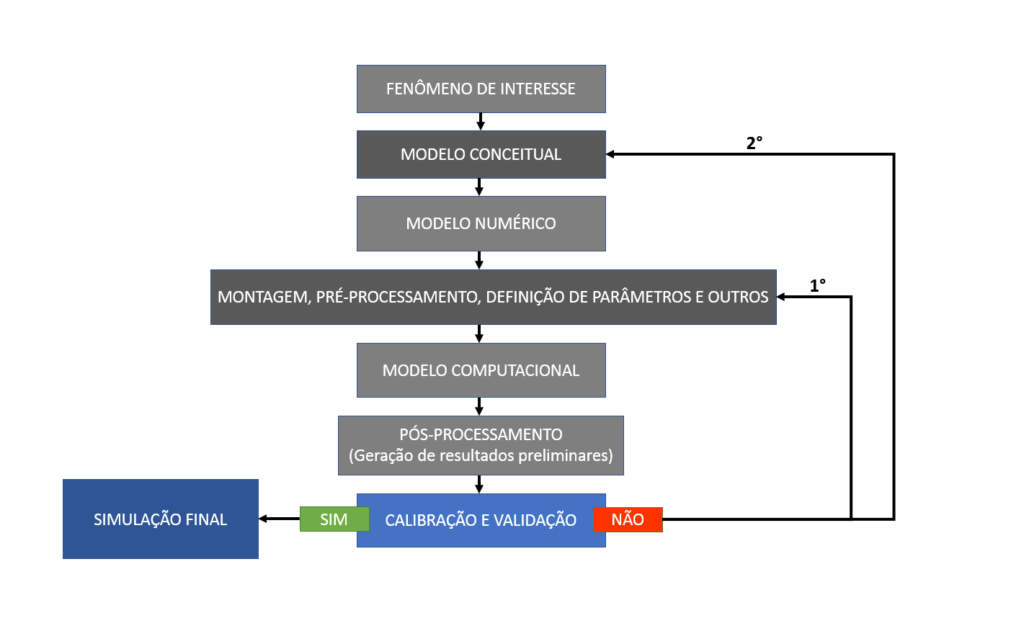
Como pode ser visto na figura acima (Diagrama do processo de modelagem – Modificada de Rosman, 2001), se o modelo NÃO está validado, existem duas rotas possíveis.
A mais comum é a 1° rota curta que leva à caixa do pré-processamento, o que corresponde ao usual procedimento de calibração via ajustes de montagem, de parâmetros aplicados nas principais equações do modelo e acertos das condições de contorno e dados de entrada.
A menos comum, é a 2° rota longa levando novamente para o modelo conceitual. Esta rota é seguida apenas no caso de repetidos insucessos de validação do modelo com a rota curta. Neste caso há que se questionar coisas mais fundamentais, e verificar se não há erro de concepção. Falamos do modelo conceitual no post 3 dessa série.
Por exemplo: no seu modelo conceitual em uma região costeira você despreza uma descarga hidrológica próxima a área de interesse por acreditar que tal vazão não seja relevante para o padrão hidrodinâmico local. Mas ao confrontar os dados simulados com os medidos, mesmo após diversos ajustes referentes a rota curta, você não consegue reproduzir o padrão das correntes. Talvez seu modelo conceitual precise ser reavaliado e tal forçante incluída.
Naturalmente que a precisão de um modelo numérico depende de um elevado número de fatores que são importantes conhecer e controlar. Essencialmente, pode-se apontar as seguintes fontes de erros de um modelo numérico:
- Ocorrência de processos físicos não descritos pelas equações do modelo;
- Escalas do modelo e do fenômeno;
- Geometria do domínio;
- Condições de contorno (forçamentos);
- Valores de parâmetros e coeficientes importantes aplicados nas equações.
1. Processos físicos não descritos pelas equações do modelo
Este é um erro que tem origem na escolha do modelo para representar o fenômeno de interesse. Existe uma etapa que antecede a implementação do modelo que é a definição do modelo a ser utilizado. É importante que você tenha certeza que o modelo escolhido atenda as suas necessidades.
Pra isso é importante verificar o conjunto de equações em que o modelo se baseia. Se você não tem o conhecimento necessário para avaliar a partir desse arcabouço teórico, uma forma é pesquisar quais modelos tem sido mais utilizados pela academia e empresas para estudar o seu fenômeno de interesse. Este já será um bom indício de quais são os melhores modelos para avaliar determinados ambientes e processos.
2. Escala
O mais fundamental passo de “calibração” é checar se as escalas características dos fenômenos de interesse e as escalas de discretização do modelo são compatíveis. Aliás isso deveria ser feito por ocasião da discretização da grade do modelo, mas frequentemente passa desapercebido pelo modelador menos experiente.
Um modelo tem escalas de discretização compatíveis com um fenômeno de interesse quando o modelo pode resolver o fenômeno. Nesse sentido, deve-se lembrar que, se um determinado fenômeno de interesse tem escalas espaciais e temporais características dadas por Δs e Δt, para se resolver tal fenômeno, as escalas de discretização do modelo devem ser pelo menos 4 vezes menor, ou seja, Δs/4 e Δt/4. Na verdade, para resolver bem tal fenômeno, e de fato ser passível de confrontação com dados medidos, o modelo deve ter uma malha com espaçamento entre os nós menor que Δs/8, e deve usar passos de tempo inferiores a Δt/8.
Frequentemente quando os resultados do modelo não representam bem os dados medidos, parte das causas está na discretização espacial e/ou temporal “inadequada”, estas são muito grosseiras para resolver o fenômeno.
3. Geometria (malha batimétrica)
O terceiro passo fundamental é checar exaustivamente se a geometria do domínio de interesse está adequadamente representada. Neste sentido, as principais ocorrências são: discretização inadequada, sempre muito grosseira para capturar feições geométricas que possam afetar os dados medidos e os resultados do modelo. E, valores
impróprios de profundidade, especialmente ao longo dos contornos, ao longo dos nós de ilhas e de canais estreitos. Por estranho que posa parecer, não é raro ter-se modelos baseados em levantamentos batimétricos antigos, tendo resultados comparados com dados recentes sem que uma atualização da batimetria tenha sido efetivada.
Pequenas diferenças em batimetria podem interferir muito significativamente em valores locais de velocidades. Em corpos de água naturais os processos sedimentológicos podem mudar significativamente a batimetria em relativamente pouco tempo e isso pode afetar enormemente as velocidades medidas.
4. Condições de contorno
O quarto e igualmente fundamental passo no processo de calibração, refere-se às condições de contorno. Uma verificação abrangente deve ser feita, porque os modelos hidrodinâmico e de transporte são muito sensíveis a mudanças nas condições de contorno. Nesse sentido, como mostrado no segundo passo, deve-se dar atenção especial às escalas características dos dados de entrada. Por exemplo:
Se os dados de vento fornecidos ao modelo têm intervalo de ΔtW entre os valores, não se pode esperar que o modelo reproduza com grande acurácia fenômenos causados por variações de vento com escala de tempo inferiores a 8ΔtW. Também, se os dados de vento fornecidos ao modelo forem uniformes no espaço, não se pode esperar que o modelo reproduza efeitos de vento local. Com relação a este último aspecto especial atenção deve ser dada em regiões com montanhas próximas do domínio de modelagem.
Outro exemplo: se os dados de elevação de nível d’água fornecidos aos nós do contorno aberto do modelo foram medidos em intervalo de tempo de ΔtT, não se pode esperar que o modelo reproduza corretamente fenômenos causados por variações do nível d’água com escala de tempo inferior a 8ΔtT. Consequentemente, se forem fornecidos dados (corretamente) medidos a cada 15 minutos, pode-se esperar que o modelo reproduza adequadamente todos os fenômenos com períodos característicos superiores a cerca de 120 minutos, ou 2 horas. Fenômenos com períodos menores que 2 horas até 60 minutos poderiam ser resolvidos, porém com menor acurácia. E fenômenos com períodos na faixa entre 30~60 minutos seriam pobremente resolvidos pelo modelo. Fenômenos com períodos inferiores a 30 minutes não poderiam ser resolvidos.
5. Parâmetros e coeficientes
As equações resolvidas pelo modelo numérico utilizam uma série de parâmetros e coeficientes em suas formulações. Alguns deles se relacionam com características específicas do ambiente e interferem diretamente no resultado gerado. Portanto, é importante compreender o que representam estes principais parâmetros e quais são os valores indicados para a sua simulação especificamente.
Os principais parâmetros e coeficientes que normalmente precisam ser ajustados no processo de calibração, são:
- Coeficiente de arrasto do vento: tal valor indica o quanto de energia do vento é transferido para a superfície da água, consequentemente, influencia diretamente na intensidade e direção das correntes superficiais. Este coeficiente pode ser constante ou linearmente dependente da velocidade do vento, refletindo o aumento rugosidade da superfície da água com o aumento da velocidade do vento;
- Rugosidade de fundo: é um parâmetro que indica em síntese qual será a força de resistência imposta ao escoamento pelo fundo do ambiente simulado. Logo, este valor terá relação direta com a batimetria (profundidade e declividade) e propriedades do material de fundo;
- Parâmetros de turbulência: estes valores só devem ser alterados (geralmente os parâmetros de viscosidade e difusividade) quando se tem certeza que todos os ajustes até aqui citados já foram realizados.
A etapa da calibração é uma das mais importantes de todo o processo de implementação do modelo. É importante que ela seja realizada com a calma e seriedade requerida. Já que a confiabilidade de todos os resultados e cenários gerados nas simulações deste modelo dependerão da execução desta fase.
A precisão final de qualquer modelo numérico é muito difícil de quantificar. Certos erros provenientes de algumas daquelas fontes poderão ser minimizados; outros, porém, terão de ser aceitos, devendo os resultados do modelo ser interpretados tendo estes aspectos em consideração.
Para elaborar este post foram utilizados os livros abaixo:
ROSMAN, P. C. C. Um Sistema Computacional de Hidrodinâmica Ambiental – Capítulo 1 (pp 1-161) do livro Métodos Numéricos em Recursos Hídricos, Vol. 5. Editora ABRH e Fundação COPPETEC. 2001.
Do Carmo, J. S. A. Modelagem em hidráulica fluvial e ambiente. Imprensa da Universidade de Coimbra. 2004.
